SAVT Rätsel zum Grübeln – Reaktor #136
Diesmal hat der SAVTi von einem Teekesselchen gehört. Leider kennt er die Lösung nicht. Kannst du ihm vielleicht weiterhelfen? Er sucht ein Wort, welches auf beide Aussagen zutrifft. (Diese Art von Rätsel nennt sich Teekesselchen)
- Wenn sich die Luft bewegt, bewege ich mich mit der Luft.
- Wenn mich jemand im Mund hat und den Mund aufmacht, stinkt es.
SAVT Rätsel zum Grübeln – Reaktor #134
Beim SAVT Verein wird immer gern im Reaktor gezündelt. Dabei steht oft ein SAVT Mitglied vor einer Anordnung an Streichhölzern und möchte genau 4 Streichhölzer umlegen, sodass 3 Quadrate entstehen. Kannst du dem SAVT Mitglied weiterhelfen?
SAVT Rätsel zum Grübeln – Reaktor #133
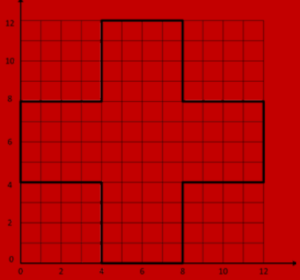
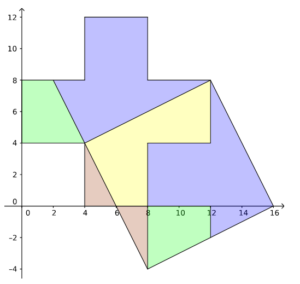
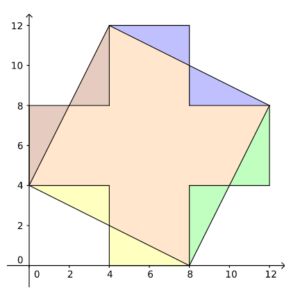
Der SAVT-Vorstand hat ein Problem: Einige Fehldrucke des neuen Reaktors wurden in Plus-förmigen Broschüren ausgeliefert und sind möglichst platzsparend zu entsorgen. Um Zeit zu sparen sollen die Exemplare mit nur zwei, oder maximal vier Schnitten so zerteilt werden, dass sich die Teile zu einem Quadrat zusammensetzen lassen.
Wie kann der Vorstand dieses Plus-Zeichen mit vier geraden Schnitten, oder mit zwei geraden Schnitten, zerschneiden, so dass man die entstandenen Teile zu einem Quadrat zusammensetzen kann?
SAVT Rätsel zum Grübeln
Der SAVT-Vorstand hat leider den Code für den SAVT-Tresor vergessen, in
dem sich die Einladungen zur Generalversammlung am 19.1.2021 befinden. Er
weiß lediglich noch, dass alle Ziffern von 1 bis 9 genau einmal vorkommen. Der
Code hat also die Form ABCDEFGHI. Außerdem hat er noch einen kleinen
Zettel mit folgenden Notizen gefunden:
E – I = F
I + E = B
G * I = A
H – C = D/I
Bestimmen Sie den Code!
Lösung:
SAVT Rätsel zum Grübeln
Wenn eine bestimmte Zahl zwischen zwei der Zahlen
eingefügt wird, ergibt sich eine Kreissequenz.
Welche Zahl muss an welcher Stelle eingefügt werden?
SAVT Rätsel zum Grübeln
Das magische Quadrat
– 3 mal 3 Felder
– Jede Zahl darf nur einmal eingesetzt werden.
– Die Summe aus allen Spalten, Zeilen und
Diagonalen muss 15 ergeben.
SAVT Rätsel zum Grübeln
A train goes between Chicago and New York. The brakeman, the fireman and
the SAVT-member are named Smith, Jones and Brown. (The names are not
necessarily in order). There are also three passengers named Mr. Smith, Mr.
Jones and Mr. Brown. Mr. Brown lives in New York. The brakeman lives halfway
between New York and Chicago. Mr. Jones earns exactly $20,000 per year. Smith
beat the fireman at their last game of golf. The passenger who lives in Chicago
has the same name as the brakeman. The brakeman‘s next door neighbor is a
passenger on this train and earns exactly three times as much as the brakeman.
What is the name of the SAVT-member?
SAVT Rätsel zum Grübeln
Es steckt mitten im Essen
Man findet es vorne im Auto
Und hinter jedem Motiv
Jedoch am häufigsten in einer Balletttruppe…
Was ist gesucht?
_ _ _ _
SAVT Mitglieder mit zweifelhaften Motiven
Es gibt drei besondere SAVT Mitglieder, eines kann es sich nicht verkneifen
immer zu lügen, eines sagt immer die Wahrheit egal zu welcher Frage, und
ein drittes gibt immer eine zufällige Antwort. Nun ist es deine Aufgabe durch
stellen von drei Fragen, herauszufinden welches Mitglied welches ist.
*Die Frage wird immer nur einem der drei gestellt
*Eine Frage kann auch mehrmals an das selbe Mitglied gerichtet werden
Ist euch das Rätsel zu einfach? Stellt euch für die SAVT Mitglieder antworten
in ihrer eigenen Sprache zB mit Dal und Bal, ihr wisst jedoch nicht welches
der Wörter ja und welches nein bedeudet.
SAVT Rätsel zum Grübeln
If you throw me out of the window,
I‘ll leave a grieving wife.
Bring me back, but through a door,
You‘ll see someone giving life.
What am I?
SAVT Rätsel zum Rechnen
Wie viel größer muss der SAVT Vorstand (17 Personen zurzeit) noch werden, sodass zwei Vorstands-Mitglieder denselben Geburtstag haben, mit einer Wahrscheinlichkeit von mindestens 50%? Selber Geburtstag bedeutet am gleichen Tag und Monat (Jahr ist irrelevant).
Lösung:
SAVT Rätsel zum Grübeln
Antwort: „n“
throw me out the window -> widow
bring me back, but through a door -> donor
SAVT Rätsel zum Rechnen
Antwort: 6 zusätzliche Vorstandsmitglieder, 17+6 = 23 und eine Gruppe von 23 Personen hat eine Wahrscheinlichkeit von mind. 50%, dass zwei Personen am selben Tag Geburtstag haben. Siehe: https://de.wikipedia.org/wiki/Geburtstagsparadoxon
SAVT Mitglieder Diamantenraub
Sieben SAVT Mitglieder übten sich als Diamantendiebe. Nach ihrem ersten Beutezug waren sie hundemüde und legten sich in der SAVT Zentrale schlafen.
Zwei SAVT Mitglieder wachten jedoch in der Nacht auf, und entschieden die Diamanten unter sich gleich aufzuteilen. Es blieb jedoch genau ein Diamant übrig. Um einen Streit zu vermeiden weckten sie also ein weiteres Mitglied auf. Beim Aufteilen blieb jedoch wieder genau ein Diamant übrig.
Also wurde ein weiteres Mitglied aufgeweckt, aber wieder blieb ein Diamant übrig. Dies wiederholte sich bis der siebte Dieb ebenfalls aufgeweckt wurde, erst dann ging es sich exakt aus.
Wieviele Diamanten haben die SAVT Mitglieder gestohlen?
Lösung:
301 Diamanten
Wir benötigen eine Zahl die ein vielfaches von 7 ist, und einen Rest von 1 aufweist bei der Division durch 2, 3, 4, 5, und 6. Das kleinste gemeinsame vielfache dieser Zahlen ist 60.
Also:
60 +1 =61 nicht vielfaches von 7
60 x 2 +1 =121 nicht vielfaches von 7
……..
60 x 5 + 1 = 301 vielfaches von 7
SAVT Mitglieder hinter Gittern
Bei einem äußerst unglücklichen Missverständnis werden 100 SAVT Mitglieder
zu lebenslanger Haft verurteilt. Sie erhalten allerdings eine Chance diese
Strafe aufzuheben. Sie werden zuerst für eine bestimmte Zeit in eine gemeinsame
Zelle gesperrt und dürfen sich dort ein System für die nachfolgende
Prozedur und Aufgabe ausdenken:
Die 100 SAVT Mitglieder werden in 100 isolierten Einzelzellen untergebracht,
von denen aus keine Möglichkeit besteht, miteinander zu kommunizieren.
Zu jeder vollen Stunde wird einer von ihnen vollkommen zufällig
ausgewählt und in einen Raum mit einer Lampe und deren Schalter geführt.
Dort DARF er den Schalter betätigen (Lampe ein/aus). Während dieser Prozedur
besteht keine Möglichkeit, den anderen Gefangenen andere Hinweise
zu hinterlassen (z. B. Strichliste an der Wand, etc.) oder mit ihnen zu kommunizieren.
Es ist unbekannt ob die Lampe vor Beginn dieser Aufgabe ein
oder ausgeschalten ist!
Sobald einer der Gefangenen dem Wächter sagt, dass bereits jeder Häftling
mindestens einmal in der Zelle war und dies zutrifft, kommen alle Gefangenen
frei. Stimmt dies nicht, haben sie keine weitere Chance ihre Haft zu
verkürzen.
Können die SAVT Mitglieder ihre Freilassung erreichen? Wenn ja, wie?
Lösung:
Es wird ein Mitglied als „Der Zähler“ ernannt. Dieser ist die einzige Person welche das Licht abschalten soll. Jedes Mal wenn der Zähler in den Raum kommt und das Licht ein ist, schaltet er dieses aus und zählt einmal. Alle anderen Mitglieder haben die Aufgabe: wenn sie in den Raum kommen und das Licht ist aus, es einzuschalten. Sollte das Licht eingeschalten sein, machen diese Personen nichts. Da nun auch nicht klar ist ob das Licht zu Beginn ein oder aus ist, soll jedes Mitglied zweimal das Licht einschalten. Kommt jemand zum dritten oder jedes weitere Mal in den dunklen Raum, schaltet dieser das Licht NICHT ein und macht nichts.
Nun muss der Zähler nur bis 198 zählen und kann sich dann sicher sein, dass jeder mindestens einmal im Raum war. Alle kommen frei!
Der unauffindbare SAVT Obmann
Eine Woche vor dem großartigen SAVT Grillfest ist der SAVT Obmann nirgendwo auffindbar. Nach ausgiebiger Recherche hat der Rest des Vorstandes herausgefunden das der Obmann sich in einer der 5 riesige Boxen, welche vor dem SAVT Hauptquartier aufgetaucht sind, versteckt.
Dem Vorstand ist es nur möglich eine der 5 Boxen pro Tag zu öffnen. Der gefinkelte Obmann bewegt sich aber in der folgenden Nacht immer in eine an seine Box grenzente Box weiter, da ihm sonst die Luft ausgehen würde.
Wie soll der SAVT Vorstand nun vorgehen um den Obmann rechtzeitig vorm Grillfest zu finden?
Lösung:
Antwort: 2->3->4->2->3->4
Nehmen wir an der Obmann befindet sich am ersten Tag in einer Box mit gerader Zahl, er befindet sich also in der Box 2 oder 4. Durchsuchen wir also Box 2 und finden den Obmann nicht, muss er sich in Box 4 befunden haben. Durch seinen täglichen Box Wechsel kann er sich also nur in Box 3 oder 5 befinden. Durchsuchen wir also als nächstes Box 3 und finden ihn nicht, war der Obmann in Box 5. Durch seine tägliche Bewegung muss er von Box 5 jedoch wieder in Box 4 wandern, wo wir ihn schlussendlich finden würden.
Der Obmann muss sich aber am Beginn der Suche sich nicht in einer Box mit gerader Nummer befunden haben, deshalb müssen wir dieses Szenario auch noch behandeln. Hat sich der Chefredakteur am Beginn in einer Box mit ungerader Nummer befunden, so befindet er sich nach den drei benötigten Tagen für das oben genannte Schema in einer Box mit gerader Nummer (Er alterniert, egal in welche Richtung er sich bewegt, immer zwischen Boxen mit gerader und ungerader Nummer).
Dadurch können wir unser Schema für gerade Boxen wieder anwenden. Und nach erneuter Prüfung von 2,3 und 4 haben wir ihn schließlich sicher gefunden.
MC-SAVT Fast Food
Das MC-SAVT Fast Food Restaurant verkauft Chicken Nuggets in den Porti-
onsgrößen 6, 9 und 20.
Was ist die größte Menge an Chicken Nuggets welche nicht durch Linear-
kombination der drei Portionsgrößen bestellt werden kann?
Di Maus in der Bibliothek
Ein Bibliothekar untersucht 3 alte Bände die geordnet von Band 1 bis Band 3 in einem Regal stehen. Er bemerkt, dass eine Maus von der 1. Seite des ersten Bandes bis zur letzen Seiten des letzten Bandes geknabbert hat. Alle Bände bestehen aus genau 100 Blatt Papier.
Wie viele Blätter hat die Maus ruiniert?
Wer Lügt?
Was für ein seltsames Dorf! Jeder Einwohner ist entweder ein notorischer Lügner, oder er sagt stets die Wahrheit. Außerdem ist jeder Einwohner Anhänger genau eines der vier Fußballvereine A, B, C und D, die es in dem Dorf gibt. Ein Meinungsforschungsinstitut hat allen 250 Dorfbewohnern die folgenden vier Fragen gestellt:
- Sind Sie Anhänger von Team A?
- Sind Sie Anhänger von Team B?
- Sind Sie Anhänger von Team C?
- Sind Sie Anhänger von Team D?
Auf die erste Frage antworteten 90 mit Ja, auf Frage zwei gab es 100 Ja-Antworten, bei Frage drei und vier waren es jeweils 80.
Lösung:
Jemand, der die Wahrheit sagt, wird eine Frage mit Ja beantworten und drei Fragen mit Nein. Ein Lügner hingegen wird einmal Nein antworten und dreimal Ja sagen. Jeder Wahrheitsliebende liefert genau eine Jastimme, jeder Lügner gibt drei Jastimmen ab.
Wenn W die Anzahl der Wahrheitsliebenden ist und L die Anzahl der Lügner, dann muss die Summe aller Jastimmen genau W + 3L entsprechen. Die Summe der Jastimmen lässt sich leicht ausrechnen:
- Sind Sie Anhänger von Team A? 90x Ja
- Sind Sie Anhänger von Team B? 100x Ja
- Sind Sie Anhänger von Team C? 80x Ja
- Sind Sie Anhänger von Team D? 80x Ja
Jastimmen = 90 + 100 + 80 + 80 = 350. Außerdem wissen wir, dass W + L = 250 sein muss, denn das Dorf hat 250 Einwohner. Daraus ergibt sich folgendes Gleichungssystem:
W + L = 250
W + 3L = 350
Daraus folgt L = 50.
Das Einsteinrätsel
Fünf Häuser stehen nebeneinander. In ihnen wohnen Menschen von fünf unterschiedlichen Nationalitäten, die fünf unterschiedliche Getränke trinken, fünf unterschiedliche Zigarettenmarken rauchen und fünf unterschiedliche Haustiere haben.
• Der Brite lebt im roten Haus.
• Der Schwede hält sich einen Hund.
• Der Däne trinkt gern Tee.
• Das grüne Haus steht (direkt) links neben dem weißen Haus.
• Der Besitzer des grünen Hauses trinkt Kaffee.
• Die Person, die Pall Mall raucht, hat einen Vogel.
• Der Mann im mittleren Haus trinkt Milch.
• Der Bewohner des gelben Hauses raucht Dunhill.
• Der Norweger lebt im ersten Haus.
• Der Marlboro-Raucher wohnt neben der Person mit der Katze.
• Der Mann mit dem Pferd lebt neben der Person, die Dunhill raucht.
• Der Winfield-Raucher trinkt gern Bier.
• Der Norweger wohnt neben dem blauen Haus.
• Der Deutsche raucht Rothmanns.
• Der Marlboro-Raucher hat einen Nachbarn, der Wasser trinkt.
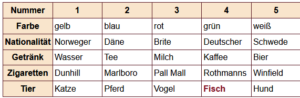
Finden Sie heraus, wem der Fisch gehört!
Lösung:
Den genauen Weg zur Lösung finden Sie hier.
Streichhölzer Rätsel
Wie kann man sechs gleich lange, gerade Linien (Streichhölzer) so miteinander verbinden, dass jede Linie an jedem ihrer beiden Enden zwei andere Linien berührt?
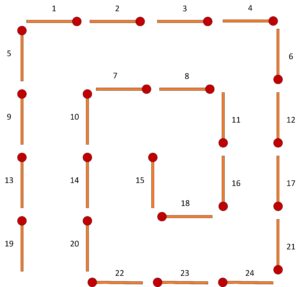
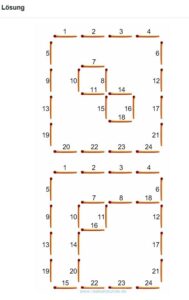
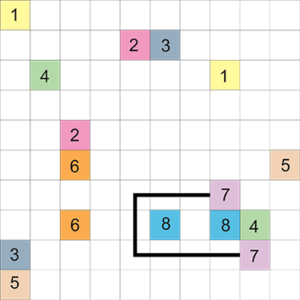
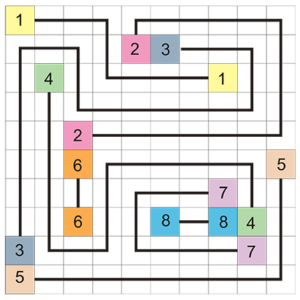
Arukone
Arukone ist ein japanisches Logikrätsel. Ziel des Spieles ist es, alle Felder mit Zahlen so miteinander zu verbinden, dass folgende Regeln gelten:
- Alle Felder mit gleicher Zahl müssen miteinander durch eine einzige, durchgehende Linie verbunden sein.
- An jedem Feld mit einer Zahl beginnt oder endet nur genau eine Linie.
- Linien dürfen nur ortogonal gezogen werden (nicht diagonal)
- Jedes Feld darf nur eine Linie beinhalten
Die Logiker des Königs
Das Geld wird knapp am Hofe und der König muss sparen. Auf die opulenten Feste und sein großes Gestüt will er natürlich nicht verzichten. Und so geraten die Stellen der zehn Logiker auf die Streichliste, die den König schon seit Jahren beraten, meist beim Schachspielen.
Er will ihnen aber eine Chance geben, ihre gut dotierten Jobs behalten zu können. dazu müssen sie müssen nur die folgende Aufgabe lösen:
„Ihr stellt euch in einer Reihe der Größe nach auf. Links der größte, rechts der kleinste. Jeder blickt in Richtung der Kleineren und darf sich weder umdrehen noch aus der Reihe heraustreten. Dann setze ich jedem einen schwarzen oder weißen Hut auf. Den eigenen Hut könnt ihr nicht sehen, nur die aller vor euch stehenden.
Jeder soll die Farbe seines Hutes sagen, beginnend links mit dem Größten. Erlaubt sind nur die Worte schwarz oder weiß. Ihr habt fünf Minuten, euch kurz zu beraten – dann müsst ihr euch aufstellen und bekommt die Hüte aufgesetzt.
Wenn mindestens neun von euch zehn die richtige Farbe nennen, dürft ihr weiter am Hofe für mich arbeiten.“
Die zehn Logiker schauen ratlos und beginnen sich zu beraten.
Wie können sie ihre Jobs behalten?
Lösung:
Dieses Rätsel ist ähnlich dem „prisoner hat riddle“ von TED-Ed, eine ausführliche Erklärung der Lösung findet ihr hier: https://www.youtube.com/watch?v=N5vJSNXPEwA
Vier Forscher im Sand
Vier Wüstenforscher, nennen wir sie A, B, C und D, werden eines Tages von einem Wüstenvolk gefangen genommen. Sie werden bis zum Kopf in einer Reihe mit Blick in die selbe Richtung im Sand eingegraben und bekommen jeder einen Hut auf. Keiner von ihnen kann den Kopf bewegen oder seine eigene Hutfarbe erkennen.
A kann B und C sehen. B kann nur C sehen. Zwischen C und D befindet sich ein Felsen. Beide können also keinen der anderen sehen. Der Anführer des Wüstenvolkes stellt ihnen folgende Bedingung: „Es gibt genau zwei weiße und zwei schwarze Hüte. Wenn einer in den nächsten 10 Minuten seine eigene Hutfarbe nennen kann, so kommt ihr alle frei. Läuft die Zeit ab oder ist die genannte Farbe falsch, werden alle getötet.“
Nach fünf Minuten löst einer das Rätsel und sagt seine eigene Hutfarbe.
Wer und wie hat er es gemacht?
Lösung:
Es gibt 2 Möglichkeiten:
- Forscher A sieht 2 gleiche Hüte auf B und C. Dadurch weiß er genau welche Farbe sein Hut haben muss.
- Forscher A sieht 2 unterschiedliche Hüte, und kann nicht auf seine Hutfarbe schließen. Durch das Schweigen von A erkennt B dass er einen unterschiedlichen Hut aufhat als C und kann seine Hutfarbe nennnen.
Einsteinrätsel
Fünf Häuser stehen nebeneinander. In ihnen wohnen Menschen von fünf unterschiedlichen Nationen, die fünf unterschiedliche Getränke trinken, fünf unterschiedliche Zigarettenmarken rauchen und fünf unterschiedliche Haustiere haben.
- Der Brite lebt im roten Haus.
- Der Schwede hält sich einen Hund.
- Der Däne trinkt gern Tee.
- Das grüne Haus steht (direkt) links neben dem weißen Haus.
- Der Besitzer des grünen Hauses trinkt Kaffee.
- Die Person, die Pall Mall raucht, hat einen Vogel.
- Der Mann im mittleren Haus trinkt Milch.
- Der Bewohner des gelben Hauses raucht Dunhill.
- Der Norweger lebt im ersten Haus.
- Der Marlboro-Raucher wohnt neben der Person mit der Katze.
- Der Mann mit dem Pferd lebt neben der Person, die Dunhill raucht.
- Der Winfield-Raucher trinkt gern Bier.
- Der Norweger wohnt neben dem blauen Haus.
- Der Deutsche raucht Rothmanns.
- Der Marlboro-Raucher hat einen Nachbarn, der Wasser trinkt.
Wem gehört der Fisch?